Consciousness of the Real — Fundamental Structure

In Consciousness of the Real, we saw that the whole of reality could be the product of one and the same substance: THAT — dynamic and self-complexifying. This substance is not passive: by unfolding along various dimensional axes, it gives rise not only to spaces but also to all fundamental physical notions. The aim here is not to posit several distinct entities or forces, but to show how a single reality, exploiting different degrees of freedom, can generate the diversity of the world.

Since THAT exists at every point of the space it generates — and since this space is finite but entirely filled by that substance — we can represent each portion of space (whether spatial or temporal) as composed of multiple points of THAT. These points are not isolated, but in constant interaction.

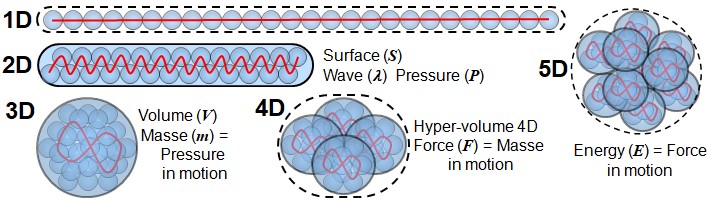
Diagram showing the increasing complexity of the substance of reality from 1D to 5D: 1D (line), 2D (surface, wave, pressure), 3D (volume, mass as pressure over a distance), 4D (4D hyper-volume, force as movement of a mass), 5D (energy as force over a distance)

Now imagine a local increase in dimensionality — a sort of contraction in certain directions — that densifies a group of points. This regrouping through complexification produces interactions, internal tensions, dynamic exchanges; in short: effects. We can represent this complexification as a progressive construction of structures, each level using more dimensional axes:

1D: a line made of points. Interaction along this line gives rise to notions like distance, speed, or acceleration.
2D: a surface made of lines of points. These lines interact within the surface, giving rise to waves, pressure, or the first forms of spatial structure.
3D: a volume formed of interactive surfaces. Here appear notions such as volume, mass (seen as pressure exerted over a distance), and the basis of material density.
4D: hyper-volume where 3D volumes (axes 1-2-3, 1-2-4, 1-3-4, 2-3-4) interact along three additional dimensions. This dynamic relation between masses gives rise to forces.
5D: forces, when acting over distances within a hyper-volume, give rise to energy — understood as force applied over distance.

In other words, at each level of contraction — or more precisely, at each level of interaction between dimensional structures — new physical notions naturally emerge. These are what we observe and measure in our reality. But there exists an even more effective way to visualize the interactions between volumes. It will soon allow us to address the question of particles — not as isolated objects, but as dynamic and relational configurations of THAT in multidimensional spaces.

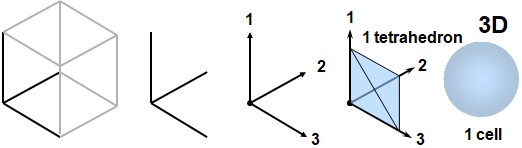
Illustration of the 3 spatial dimensions: cube in perspective, 1D, 2D, and 3D axes, formation of a tetrahedron and a spherical cell representing a 3D unit

Starting from a simple three-dimensional cube, we select three of its edges that meet at a common origin point: these are our first three dimensional axes, here labeled 1, 2, and 3. If we consider that each axis is filled with the substance THAT, then the volume defined by these three directions forms a tetrahedron (a quarter of a pyramid), which can be regarded as a cell of the substance of the real within 3D space.

This tetrahedral cell has:

3 axes (1, 2, 3) — directions of expansion of the substance,
3 surface faces (called 2-faces): the pairs 1-2, 1-3, and 2-3,,
3 volumetric face (3-face): the combination 1-2-3.

This basic cell will serve as a unit for understanding:

the internal relationships between components of a physical system,
the interactions with neighboring cells,
the genesis of notions such as force, energy, or the structure of particles.

By adding a fourth dimensional axis (axis 4) to the first three, we allow the substance THAT to occupy a new direction of expansion, opening the possibility for the coexistence of multiple volumes within a single hyperspace.

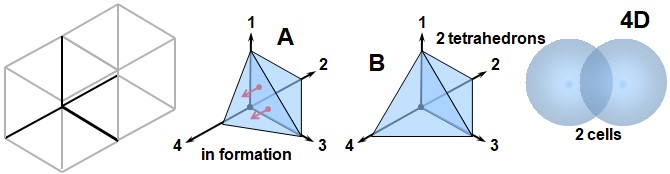
Illustration of 4D structure: stacking of two tetrahedra forming a 4D cell, representation of a 4D cube, a forming cell (A), two merged tetrahedra (B), and two spherical cells sharing a volumetric face

In Illustration A, we see two volumes (tetrahedra) — the first, based on axes 1-2-3, and the second, forming on axes 1-3-4. These two volumes share a common volumetric surface (the 1-3 face), represented here by red arrows, and can thus interact dynamically through this shared interface.

Once the formation is complete (Illustration B), the two cells are connected by this shared face, and any internal variation in density or pressure within one (such as an internal wave) can affect the other. This interaction — a motion induced in one volume by another — corresponds to what we call a force in our physical world.

Thus, force is not an addition to the physical world, but a geometrical consequence of the expansion of THAT into a fourth dimensional axis.

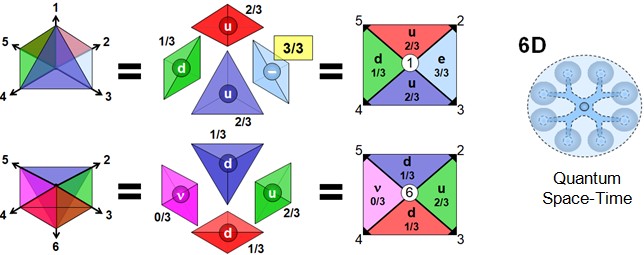
$Diagram showing two distinct configurations of spation flavors within 6-dimensional quantum spacetime. On the left: two tetrahedrons of spations numbered from 1 to 6 based on their dimensional axes, each illustrating a specific geometric combination. In the center: representations of spation flavor groupings within each tetrahedron, associated with fractional charges (1/3, 2/3, 3/3, 0/3). These combinations give rise to stable structures corresponding to different configurations of particles (electron, neutrino, up-type or down-type spation flavors). On the right: projection of the same configurations onto a two-dimensional grid, revealing their internal symmetries. In the inset: 6D quantum spacetime is depicted as a central structure connected to six directional spation axes.$

With the addition of two more axes (axes 5 and 6), the structure formed by the initial volumes becomes even more complex. One can then represent eight tetrahedral volumes, each sharing one or more edges with a central volume (formed on axes 1-2-3), allowing us to calculate how many axes each of these volumes shares with the central one.

results — 0/3, 1/3, 2/3, 3/3 — coincide exactly with the known electric charges in the Standard Model:

0/3 ⇒ neutrino (neutral)
1/3 ⇒ quark down (d)
2/3 ⇒ quark up (u)
3/3 ⇒ electron (e^-)

These configurations emerge naturally from the topology of interconnected volumes in six-dimensional space. They are therefore not arbitrary properties added to particles, but direct effects of the degree of dimensional overlap between elementary cells of THAT.

This suggests that:

Elementary particles are not localized objects, but dynamic configurations of volumes of THAT, distributed across a multidimensional space-time.
The quantum of volume/matter is not merely a "packet of energy," but a cell of reality — simultaneously a field and a form, a localization and a dynamic structure.
The strange behaviors of the quantum world (indeterminacy, superposition, entanglement…) could be naturally explained as effects of the coexistence of these cells across several intertwined spatial and temporal dimensions.

In other words, the physical world — and space-time itself — would be made of THAT, contracted and combined according to precise geometrical patterns. This implies that we — and the space we inhabit — are composed of these elementary cells, these quanta of THAT, and not of a "fabric" of empty space or separate objects. Each cell represents a quantum of volume and mass, produced by the exploitation of six spatial and temporal dimensions.

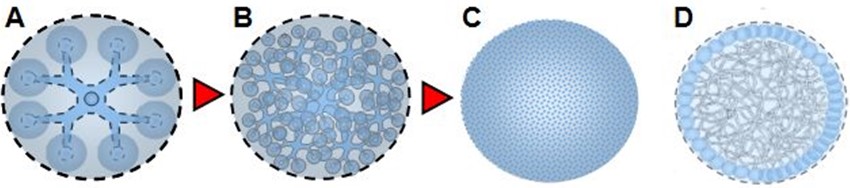
Evolution of a 6D cell: A) expanding primary structure, B) cellular complexification, C) formation of a homogeneous sphere, D) complex internal structure with high density

But it would be mistaken to imagine these cells as neatly arranged marbles or Lego bricks. These entities do not exist as fixed and localized structures, but rather as dynamic and overlapping forms, as characteristic of quantum mechanics. There is no empty space between them, no clear boundaries or rigid connections. They are entangled, subtly interconnected, and fluctuating.

Figure A — showing 8 neatly arranged cells around a center — is misleading. A more faithful representation would be that of a dense, wave-like, and foamy network, as in Figures B and C. These cells, unstable and partially defined, interact through their three-dimensional faces, but they themselves only represent the local projections of a more global, more complex object — probably inconceivable without a geometry beyond our usual space-time.

Figure D attempts to sketch this idea: a kind of quantum foam without void, where the state of one cell cannot be altered without instantly affecting other cells at a distance. This vision is compatible with the quantum entanglement observed experimentally: quanta would be local manifestations of an indivisible global system, where the modification of one link causes an immediate structural reorganization of the whole.

In other words, the world we perceive as made of separate particles and empty space would, in reality, be a vast wave composed of coordinated fluctuations of a single conscious substance — a wave incarnated in the very structure of THAT.

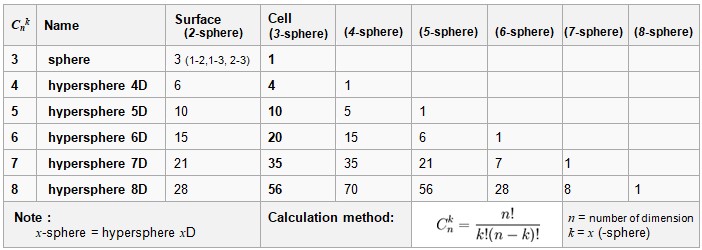
Table of hypersphere cells by dimension: number of surfaces, cells and subspheres for hyperspheres from 3D to 8D, with calculation formula Cnk = n! / (k!(n-k)!)

As the table above shows, a six-dimensional (6D) hypersphere does not contain eight, but twenty distinct three-dimensional cells. In other words, the 6D hyper-volume consists of 20 volumetric charges, each corresponding to a unique combination of three axes among the six available.

This reinforces the idea that elementary particles — such as quarks, electrons, or neutrinos — are not point-like entities, but modes of organization of these cells within a higher-dimensional space, each being a quantum of mass, energy, or interaction.

That said, to preserve the clarity of the exposition and avoid unnecessarily burdening the explanations, we will continue to use the simplified eight-cell model whenever it suffices to illustrate a principle or a structure. This minimal model remains pedagogically effective for understanding the foundations of this cosmic architecture, even if it does not capture the full richness of the underlying system.